Support Vector Machines
A
support vector machine (SVM) is a statistical supervised learning
technique from the field of machine learning applicable to both classification
and regression. The original SVM algorithm was invented by Vladimir N. Vapnik
and the current standard incarnation (soft margin) was proposed by Corinna
Cortes and Vapnik in 1993 and published 1995. [1] SVMs use the spirit of the Structural
Risk Minimization principle.
A
support vector machine constructs a hyperplane or set of hyperplanes in a high
or infinite dimensional space, which can be used for classification,
regression, or other tasks. Good separation is achieved by the hyperplane that
has the largest distance to the nearest training data point of any class
(so-called functional margin), since in general the larger the margin the lower
the generalization error of the classifier. SVMs are used to classify linear
and nonlinear separation models.
Whereas
the original problem may be stated in a finite dimensional space, it often
happens that the sets to discriminate are not linearly separable in that space.
For this reason, it was proposed that the original finite-dimensional space be
mapped into a much higher-dimensional space, presumably making the separation
easier in that space. To keep the computational load reasonable, the mappings
used by SVM schemes are designed to ensure that dot products may be computed
easily in terms of the variables in the original space, by defining them in
terms of a kernel function K(x,y) selected to suit the problem.
Structural Risk minimization
Structural
risk minimization (SRM) (Vapnik and
Chervonekis, 1974) is an inductive principle for model selection used for
learning from finite training data sets. It describes a general model of
capacity control and provides a trade-off between hypothesis space complexity
(the VC dimension of approximating functions) and the quality of fitting the
training data (empirical error). The procedure is outlined below.
- Using a priori knowledge of the domain, choose a class of functions, such as polynomials of degree n, neural networks having n hidden layer neurons, a set of splines with n nodes or fuzzy logic models having n rules.
- Divide the class of functions into a hierarchy of nested subsets in order of increasing complexity. For example, polynomials of increasing degree.
- Perform empirical risk minimization on each subset (this is essentially parameter selection).
- Select the model in the series whose sum of empirical risk and VC confidence is minimal.
Hyper plane
More
generally, a hyperplane is any codimension-1 vector subspace of a vector space.
Equivalently, a hyperplane V in a vector space W is any subspace such that W/V
is one-dimensional. Equivalently, a hyperplane is the linear transformation
kernel of any nonzero linear map from the vector space to the underlying field.
Margin
The
distance we have to travel away from the separating line (in a direction
perpendicular to the line) before we hit a data point. Representation of margin
is illustrated in figure (1).
Figure (1)
Support vectors
The
data points in each class that lie closest to the classification line. They are
the most difficult to classify. Support vectors have direct bearing on the
optimum location of the decision surface. Representation of support vectors is
illustrated in figure (2).
Figure (2)
Finding maximum margin classifier (optimal hyper plane)
Separating
hyperplane has the form  where ‘w’ is the weight vector, ‘x’ is the particular
input vector and ‘b’ is the bias.
where ‘w’ is the weight vector, ‘x’ is the particular
input vector and ‘b’ is the bias.
 where ‘w’ is the weight vector, ‘x’ is the particular
input vector and ‘b’ is the bias.
where ‘w’ is the weight vector, ‘x’ is the particular
input vector and ‘b’ is the bias.
New data points x are
classified according to the sign of y(x)
The
training data set comprises N input vectors  with corresponding target values
with corresponding target values  where
where  and new data points are classified according to the
sign of y(x).
and new data points are classified according to the
sign of y(x).
 with corresponding target values
with corresponding target values  where
where  and new data points are classified according to the
sign of y(x).
and new data points are classified according to the
sign of y(x).
The distance from A to the
separating plane is given by below equation (2)
The
separation margin should be in minimum distance. Therefore the margin (M) for the given data points is given by below equation
(3)
In
support vector machines, it is needed to find the w and b that maximizes
the above margin (M). This can be written as
When
finding the optimal values of w and b, the data points should be in the correct side of the
hyperplane. Therefore, hyperplane should maximizes the margin and all data
points are correctly classified.
The above optimization
problem can be rewritten as (5) to classify all the data points correctly.
Direct
solution of this optimization problem would be very complex, and so it should
be convert into an equivalent problem that is much easier to solve.
To
do this rescaling  and
and  (where ‘k’ is a constant) can be done, then the
distance from any point
(where ‘k’ is a constant) can be done, then the
distance from any point  to the hyperplane, given by
to the hyperplane, given by  is unchanged.
is unchanged.
 (where ‘k’ is a constant) can be done, then the
distance from any point
(where ‘k’ is a constant) can be done, then the
distance from any point  to the hyperplane, given by
to the hyperplane, given by  is unchanged.
is unchanged.
Then it is
freedom to set
For
the point(s) that are closest to the hyperplane. In this case, all the data
points will satisfy the constraints
This is known as the
canonical representation of the decision hyperplane.
In
the case of data points for which the equality holds, the constraints are said
to be active, whereas for the remainder are said to be inactive.
By definition, there will always be at least one active
constraint, because there will always be a closest point, and once the margin
has been maximized there will be at least two active constraints.
The
optimization problem simply requires that we maximize , which is equivalent to minimizing
, which is equivalent to minimizing , then optimization problem can be written
as below (8)
, then optimization problem can be written
as below (8)
 , which is equivalent to minimizing
, which is equivalent to minimizing , then optimization problem can be written
as below (8)
, then optimization problem can be written
as below (8)
Subject to
the constraints
Lagrange Multipliers
In
mathematical optimization, the method of Lagrange multipliers (named after
Joseph Louis Lagrange) is a strategy for finding the local maxima and minima of
a function subject to equality constraints.
Consider the
following optimization problem (which is called as primal)
To solve
this problem first the generalized lagragian Function can be written as follows
Now consider
the quantity
P stands for
primal
It can be shown that
 takes the same value as the objective in our problem
for all values of w that satisfies the primal constraints, and is positive
infinity if the constraints are violated.
takes the same value as the objective in our problem
for all values of w that satisfies the primal constraints, and is positive
infinity if the constraints are violated.
Hence, minization problem
considered as follows.
It is the
same problem as original, primal problem.
Let’s define
the optimal value of the objective to be
This value called
as value of the primal problem.
Lagrange Duality
Now let’s
define a slightly different problem.
Here D
stands for dual
Note
that, in the definition of  , should be optimized (maximized) with respect to
, should be optimized (maximized) with respect to  and
and  (Lagrangian multipliers), and here dual problem is
minimizing with respect to
(Lagrangian multipliers), and here dual problem is
minimizing with respect to 
 , should be optimized (maximized) with respect to
, should be optimized (maximized) with respect to  and
and  (Lagrangian multipliers), and here dual problem is
minimizing with respect to
(Lagrangian multipliers), and here dual problem is
minimizing with respect to 
The dual optimization
problem can be written as follow
This
is exactly the same as our primal problem shown above (eq 16), except that the
order of the “max” and the “min” are now exchanged.
Optimal value of the dual
problem’s objective to be defined as follows
Karush–Kuhn–Tucker conditions
The method of Lagrange Multipliers is used to find the
solution for optimization problems constrained to one or more equalities. When
constraints also have inequalities, methods are extended to the Karush–Kuhn–Tucker (KKT) conditions.
Under these assumptions, there exist ,
, and
and  so that
so that  is the solution to the primal
problem and,
is the solution to the primal
problem and,  and
and  are the solution to the dual problem
are the solution to the dual problem
 ,
, and
and  so that
so that  is the solution to the primal
problem and,
is the solution to the primal
problem and,  and
and  are the solution to the dual problem
are the solution to the dual problem
Moreover, if some ,
, and
and  satisfy the KKT conditions, it is
also a solution to the primal and dual problems.
satisfy the KKT conditions, it is
also a solution to the primal and dual problems.
 ,
, and
and  satisfy the KKT conditions, it is
also a solution to the primal and dual problems.
satisfy the KKT conditions, it is
also a solution to the primal and dual problems.
Eq (23) is called the KKT dual complementarity condition.
Specially, it implies that if , then
, then  (i.e. the constraint
(i.e. the constraint  is active, meaning it holds the
equality rather than inequality).
is active, meaning it holds the
equality rather than inequality).
 , then
, then  (i.e. the constraint
(i.e. the constraint  is active, meaning it holds the
equality rather than inequality).
is active, meaning it holds the
equality rather than inequality).
Lagrangian function
 should be minimize with respect to w
and b, and which will be done by setting derivatives of
should be minimize with respect to w
and b, and which will be done by setting derivatives of  w.r.t.
w.r.t.  and
and  to zero.
to zero.
Then
Using (27)
following equation (29) can be obtained
Substituting
to equation (26) following equation (30) can be obtained
Dual problem
This
is also a quadratic programming problem in which maximize a quadratic function
of  subject to some linear constraints.
subject to some linear constraints. can be found by solving above dual problem.
can be found by solving above dual problem.
 subject to some linear constraints.
subject to some linear constraints. can be found by solving above dual problem.
can be found by solving above dual problem.
For a novel input vector
x, the predicted class is then based on the sign of
Kernels
The
kernel trick was first published by Aizerman, Braverman and Rozonoer [2].Mercer's theorem states that any continuous, symmetric, positive semi definite kernel
function K(x; y) can be expressed as a dot product in a high
dimensional space.
The
idea of the kernel function is to enable operations to be performed in the
input space rather than the potentially high dimensional feature space. Hence
the inner product does not need to be evaluated in the feature space. We want the
function to perform mapping of the attributes of the input space to the feature
space. The kernel function plays a critical role in SVM and its performance.
See figure (3)

Figure (3)
Kernel
function should be satisfy below conditions to be valid kernel.
- Symmetric ;

- Positive definite; for any
 , the Gram matrix K must be positive
semi-definite:
, the Gram matrix K must be positive
semi-definite:Some Kernel functions
Radial Basis
Kernel function
Polynomial
Kernel function
Sigmoid
function
Multi Class classification
SVMs
were developed to perform binary classification. However, applications of
binary classification are very limited especially in remote sensing land cover
classification where most of the classification problems involve more than two
classes. A number of methods to generate multiclass SVMs from binary SVMs have
been proposed by researchers and is still a continuing research topic.
One against rest
This
method is also called winner-take-all classification. Suppose the
dataset is to be classified into M classes. Therefore, M binary
SVM classifiers may be created where each classifier is trained to distinguish
one class from the remaining M-1 classes. For example, class one binary
classifier is designed to discriminate between class one data vectors and the
data vectors of the remaining classes. Other SVM classifiers are constructed in
the same manner. During the testing or application phase, data vectors are
classified by finding margin from the linear separating hyperplane. The final
output is the class that corresponds to the SVM with the largest margin.
One against one
In
this method, SVM classifiers for all possible pairs of classes are created [3], [4].Therefore, for M classes, there will be binary classifiers. The output
from each classifier in the form of a class label is obtained. The class label
that occurs the most is assigned to that point in the data vector. In case of a
tie, a tie-breaking strategy may be adopted. A common tie-breaking strategy is
to randomly select one of the class labels that are tied. This method is
considered more symmetric than the one against-the-rest method.
Multiclass objectives function
Instead of creating many binary classifiers to determine the class labels, this method attempts to directly solve a multiclass problem [5] [6] [7]
This
is achieved by modifying the binary class objective function and adding a
constraint to it for every class. The modified objective function allows
simultaneous computation of multiclass classification and is given by [6]
Subject
to the constraints
For
and
Decision Directed Acyclic Graph based Approach
Platt [8] proposed a multiclass classification method called Directed Acyclic Graph SVM (DAGSVM) based on the Decision Directed Acyclic Graph (DDAG) structure that forms a tree-like structure. The DDAG method in essence is similar to pairwise classification such that, for an M class classification problem, the number of binary classifiers is equal to
 and each classifier is trained to classify two
classes of interest. Each classifier is treated as a node in the graph
structure. Nodes in DDAG are organized in a triangle with the single root node
at the top and increasing thereafter in an increment of one in each layer until
the last layer that will have M nodes. See figure (4)
and each classifier is trained to classify two
classes of interest. Each classifier is treated as a node in the graph
structure. Nodes in DDAG are organized in a triangle with the single root node
at the top and increasing thereafter in an increment of one in each layer until
the last layer that will have M nodes. See figure (4)
Figure (4)
References
[1]
|
Cortes, Corinna and Vapnik, Vladimir,
"Support-vector networks," Machine Learning, vol. 20, no. 3,
pp. 273-297, 1995.
|
[2]
|
AIZERMAN, M. A., E. M. BRAVERMAN, and L. I.
ROZONOER, "Theoretical foundations of the potential function method in
pattern recognition learning," Automation and Remote Control, Vol. 25
(1964), pp. 821-837 Key: citeulike:431797, vol. 25, no. 6, pp. 821-837,
1964.
|
[3]
|
T. J. Hastie and R. J. Tibshirani,
"Classification by pairwise coupling," Advances in Neural
Information Processing Systems, vol. 10, 1998.
|
[4]
|
Knerr, S., Personnaz, L. and Dreyfus, G.,
"Single-layer learning revisited: A stepwise procedure for building and
training neural network.," Neurocomputing: Algorithms, Architectures
and Applications, 1990.
|
[5]
|
J. Weston and C. Watkins, "Multi-class Support
Vector Machines," Royal Holloway, University of London, 1998.
|
[6]
|
Lee, Y., Lin, Y. and Wahba, G., "Multicategory
support vector machines," Department of Statistics, University of
Wisconsin, Madison, WI, 2001.
|
[7]
|
Crammer, K. and Singer, Y., "On the algorithmic
implementation of multiclass kernel-based vector machines.," Journal
of Machine Learning Research, vol. 2, pp. 265-292, 2001.
|
[8]
|
J. Platt, N. Cristianini and J. Shawe-Taylor,
"Large margin DAGs for multiclass classification.," Advance in
Neural Information Processing Systems, vol. 12, pp. 547-553, 2000.
|
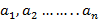








































































Great Article.
ReplyDeleteCool article!!!
ReplyDeleteI really liked your blog article.Really thank you! Really Cool.
ReplyDeleteAppreciate you sharing, great article.Much thanks again. Really Cool.
Thanks for the blog article.Thanks Again. Keep writing.
I really liked your blog post.Much thanks again. Awesome.
machine learning course in hyderabad
best machine learning course in india